On constate expérimentalement, en renversant sur une planche le contenu du couvain d’une fourmilière, que les fourmis trient spontanément les oeufs par stades d’évolution : elles font de petits tas d’oeufs, de larves et de nymphes. Elles sont même capables de distinguer plusieurs stades d’évolution pour les oeufs. Comment peut-on expliquer ce comportement complexe alors qu’une fourmi est un être très simple ? Nous allons voir dans cet article que l’on peut modéliser par ordinateur ce comportement observé par les anthomologistes.

Applet Java

Si vous voyez ce texte, c’est que votre navigateur n’est pas compatible Java ou n’a pas été correctement configuré.

Réglages de l’applet

Panneau DEPART

Permet de déterminer la disposition de la position de départ : le nombre de fourmis et d’oeufs de chaque type (A et B ou Rouge et Bleus).

Panneau Règles

On y détermine le comportement d’une fourmi : les constantes K+ et K-, le type de perception (spatiale ou temporelle) et la taille de la mémoire (dans le cas de la perception temporelle) ou le rayon de recherche (dans le cas de la perception spatiale).

Attention !

Lorsqu’on change le type de perception, il ne faut pas oublier de modifier la taille de la mémoire ou le rayon de la recherche : ces valeurs sont conservées lors du changement de mode et ont des ordres de grandeur différents.

Panneau Terrain

Détermine les dimensions du terrain et du coté d’une case de la grille (en pixels). On peut aussi y régler le temps entre deux mouvements (en ms). Cette dernière options est utile pour étudier le comportement des fourmis en détail.

Lancement de la simulation

Lorsque tous les paramètres sont convenablement règlés, on lance la simulation en cliquant sur le bouton [Lancer].

Dans la fenètre de simulation, les boutons [>] et [||] permettent de lancer ou arrèter la simulation. Le compteur suivant indique le temps dans le monde de la fourmi, le bouton [Vider] réinitialise la grille et le dernier bouton permet de fermer cette fenètre.

Bonne simulation…

Le tri du couvain

Données dont dispose une fourmi sur son environnement

Les fourmis sont capables d’émettre et de capter des molécules appelées phéromones. Un oeuf de fourmi émet des phéromones différentes suivant son stade d’évolution. On peut donc légitimement supposer qu’une fourmi est capable d’estimer la concentration en oeufs du même stade au point où elle se trouve en “reniflant” les phéromones (qu’elles captent avec leurs antennes). Par contre, la myopie des fourmis leur interdit d’avoir une vue d’ensemble du couvain. On peut aussi supposer qu’une fourmi dispose d’une mémoire à court terme des oeufs qu’elle a rencontré durant les denières secondes de son déplacement.

On peut donc réaliser deux modèles de comportement : le premier suppose que la fourmi a une perception spatiale de la concentration en oeufs d’un type donné, le deuxième fait intervenir la mémoire à court terme de la fourmi.

Modélisation du comportement des fourmis

Pour modéliser le comportement de la fourmi, il nous faut simplifier l’environnement de nos fourmis virtuelles. Nous supposerons que nos fourmis se déplacent sur une grille. Sur cette grille seront disposés au début de la simulation des oeufs de 2 types : des Rouges et de Bleus.

La simulation est découpées en tours. A chaque tour, la fourmi se déplace aléatoirement sur une case adjacente (au nord, au sud, à l’est ou à l’ouest mais pas en diagonale). Lorsqu’une fourmi arrive sur une case contenant un oeuf, elle peut décider de l’emporter ou de le laisser.

Quel que soit le modèle de la perception de la concentration des oeufs, on peut établir un ensemble de règles régissant les fourmis lors du tri du couvain :

1. Si une fourmi ne portant rien rencontre un oeuf et que la concentration locale de ce type d’oeufs est faible, la fourmi aura tendance à l’emporter. Au contraire, si la concentration est forte, elle aura tendance à le laisser sur place et a continuer sa route.
2. Si une fourmi porte un oeuf et qu’elle arrive sur une case vide, elle aura tendance à déposer cet oeuf si la concentration locale de ce type est forte et à le garder si la concentration est faible.

L’applet Java présentée dans cette page modélise ce comportement et implémente les deux modèles de perception (spatial et temporelle). Vous en savez maintenant assez pour expérimenter avec cette applet. Je vous suggère de le faire par vous même avant d’étudier les résultats présentés ci-dessous.

Résultats de la simulation informatique

Les résultats de la simulation sont assez convaincants :

Perception spatiale (aux temps 0, 1000 et 10 000)

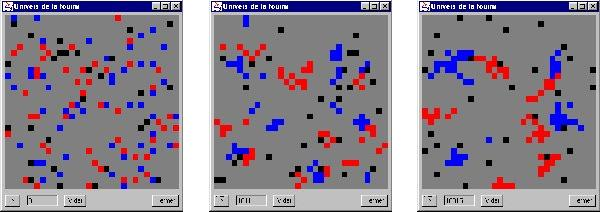
Perception temporelle (aux temps 0, 1000, 10 000)

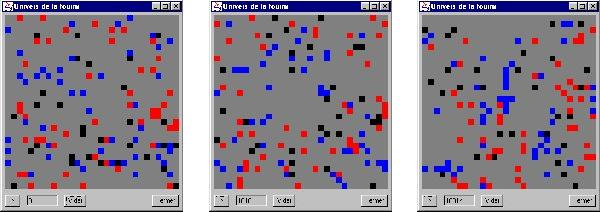
On constate bien que les oeufs sont regroupés par tas d’ouefs semblables. La méthode semble plus efficace avec une perception spatiale qu’avec la temporelle.

Conclusion

Cette simulation permet de valider les modèles du comportement de la fourmi par simulation. Même si cela ne prouve pas que ces modèles sont juste, cela permet de penser qu’ils sont efficaces et conduisent à des résultats semblables à ceux que l’on observe chez les fourmis.

Cette étude est intéressante pour les enthomologistes, mais intéresse aussi les informaticiens. En effet, cette simulation met en oeuvre une intelligence collective : à partir de comportements simples, l’ensemble des fourmis tri les oeufs, alors qu’une fourmi en est incapable seule. Cette situation de travail collectif se présente en informatique lorsqu’on fait travailler ensemble plusieurs processeurs. Chaque processeur est simple mais doit travailler avec ses voisins de manière à ce que la tâche qu’on leur a confié avance. Les avantages d’une architecture parallèle sont multiples : tout d’abord, à puissance égale, plusieurs petits processeurs coutent moins cher qu’un unique processeur plus perfectionné (c’est ce qui est mis en oeuvre dans la BeBox), d’autre part, si un processeur vient à tomber en panne, les autres peuvent continuer à fonctionner, ce qui augmente fortement la tolérance à la panne.

De toute façon, même si c’est totalement inutile, on s’amuse bien quand même ;-)

Pour en savoir plus

Cet article a été rédigé sur la base des travaux de : Guy THERAULAZ, Eric BONABEAU, Simon GOSS et Jean-Louis DENEUBOURG.

• Pour la science N°198 avril 1994, page 90.

Formules

Pour modéliser le comportement des fourmis sur ordinateur, on doit passer par un modèle mathématique (l’ordinateur ne comprend pas “la fourmi aura tendance à ramasser l’oeuf”). Pour le modèle du couvain, on doit définir 3 formules :

Concentration en oeufs d’un type

La fourmi ramasse ou dépose un oeuf en fonction de la concentration locale en oeufs du même type (Rouge ou Bleu dans le modèle). On doit donc fournir un moyen mathématique pour estimer cette concentration. Nous avons distinguer deux méthodes possibles :

Perception spatiale

Dans ce modèle, on estime la concentration en oeufs en déterminant le nombre d’oeufs du type à évaluer par rapport au nombre de cases autour de la fourmi. Dans un premier temps, il nous faut donc compter le nombre d’oeufs du type désiré dans le périmètre de recherche (on peut prendre les 8 cases entourant la fourmi plus la case sur laquelle elle se trouve), on appelle ce nombre N. M sera le nombre total de cases dans le périmètre. La concentration, notée f, sera alors le rapport :

f = N / M

Il est possible d’étendre le périmètre à un plus grand nombre de cases (par exemple les 25 cases autour de la fourmi, soit un périmètre de rayon 2).

Perception temporelle

Dans ce cas, la concentration d’oeufs est fonction du nombre d’oeufs du type recherché sur lesquels la fourmi est passé au cours de ses derniers déplacements. Pour ce faire, on rempli un tableau avec le contenu des dernières cases sur lesquelles est passée la fourmi : si elle passe sur une case vide, on note 0, si elle passe sur une case contenant un oeuf rouge, on note 1, si elle passe sur un bleu, on note 2. A chaque nouvelle case rencontrée, la nouvelle valeur chasse la plus ancienne. La taille du tableau est fonction de la mémoire de la fourmi. Une valeur de 15 est raisonnable.

On appelle alors N le nombre d’oeufs du type dont on veut estimer la concentration et M le nombre de cases dont la fourmi peut se rappeler le contenu (soit la taille du tableau). Alors, la concentration f sera :

f = N / M

Probabilité pour que la fourmi ramasse un oeuf

Lorsqu’une fourmi arrive sur une case comportant un oeuf et qu’elle a les “mains libres”, elle peut ramasser l’oeuf avec une probabilité P+. Cette probabilité est fonction de la concentration en oeufs du même type, calculée ci-dessus, f. La formule est :

P+ = (K+ / (K+ + f))²

K+ est une constante que l’on peut prendre égale à 0,1.

Cette fonction est faite de telle manière à ce que plus la concentration des oeufs (soit f) est faible, et plus la probabilité que la fourmi ramasse l’oeuf (soit P+) est voisine de 1.

Probabilité pour que la fourmi dépose un oeuf

Lorsqu’une fourmi portant un oeuf arrive sur une case vide, elle peut le déposer avec une probabilité P-. Cette probabilité est fonction de la concentration en oeufs du même type, calculée ci-dessus, f. La formule est :

P- = (f / (K- + f))²

K- est une constante que l’on peut prendre égale à 0,1.

Cette fonction est faite de telle manière à ce que plus la concentration des oeufs (soit f) est grande, et plus la probabilité que la fourmi dépose l’oeuf (soit P-) est voisine de 1.

Lorsque la fourmi arrive sur une nouvelle case, on estime la probabilité qu’elle ramasse un oeuf ou le dépose, puis on tire un nombre aléatoire réel compris entre 0 et 1, noté x. Si x est inférieur à P+ ou P-, alors la fourmi ramassera ou déposera son oeuf.